DataPreprocessing

0. Preprocessing
preprocessing.Binarizer(*[, threshold, copy]) |
Binarize data (set feature values to 0 or 1) according to a threshold. |
|---|---|
preprocessing.FunctionTransformer([func, …]) |
Constructs a transformer from an arbitrary callable. |
preprocessing.KBinsDiscretizer([n_bins, …]) |
Bin continuous data into intervals. |
preprocessing.KernelCenterer() |
Center a kernel matrix. |
preprocessing.LabelBinarizer(*[, neg_label, …]) |
Binarize labels in a one-vs-all fashion. |
preprocessing.LabelEncoder() |
Encode target labels with value between 0 and n_classes-1. |
preprocessing.MultiLabelBinarizer(*[, …]) |
Transform between iterable of iterables and a multilabel format. |
preprocessing.MaxAbsScaler(*[, copy]) |
Scale each feature by its maximum absolute value. |
preprocessing.MinMaxScaler([feature_range, …]) |
Transform features by scaling each feature to a given range. |
preprocessing.Normalizer([norm, copy]) |
Normalize samples individually to unit norm. |
preprocessing.OneHotEncoder(*[, categories, …]) |
Encode categorical features as a one-hot numeric array. |
preprocessing.OrdinalEncoder(*[, …]) |
Encode categorical features as an integer array. |
preprocessing.PolynomialFeatures([degree, …]) |
Generate polynomial and interaction features. |
preprocessing.PowerTransformer([method, …]) |
Apply a power transform featurewise to make data more Gaussian-like. |
preprocessing.QuantileTransformer(*[, …]) |
Transform features using quantiles information. |
preprocessing.RobustScaler(*[, …]) |
Scale features using statistics that are robust to outliers. |
preprocessing.StandardScaler(*[, copy, …]) |
Standardize features by removing the mean and scaling to unit variance |
preprocessing.add_dummy_feature(X[, value]) |
Augment dataset with an additional dummy feature. |
|---|---|
preprocessing.binarize(X, *[, threshold, copy]) |
Boolean thresholding of array-like or scipy.sparse matrix. |
preprocessing.label_binarize(y, *, classes) |
Binarize labels in a one-vs-all fashion. |
preprocessing.maxabs_scale(X, *[, axis, copy]) |
Scale each feature to the [-1, 1] range without breaking the sparsity. |
preprocessing.minmax_scale(X[, …]) |
Transform features by scaling each feature to a given range. |
preprocessing.normalize(X[, norm, axis, …]) |
Scale input vectors individually to unit norm (vector length). |
preprocessing.quantile_transform(X, *[, …]) |
Transform features using quantiles information. |
preprocessing.robust_scale(X, *[, axis, …]) |
Standardize a dataset along any axis |
preprocessing.scale(X, *[, axis, with_mean, …]) |
Standardize a dataset along any axis. |
preprocessing.power_transform(X[, method, …]) |
Power transforms are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. |
1. Feature discretization
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.utils._testing import ignore_warnings
from sklearn.exceptions import ConvergenceWarning
print(__doc__)
h = .02 # step size in the mesh
def get_name(estimator):
name = estimator.__class__.__name__
if name == 'Pipeline':
name = [get_name(est[1]) for est in estimator.steps]
name = ' + '.join(name)
return name
# list of (estimator, param_grid), where param_grid is used in GridSearchCV
classifiers = [
(LogisticRegression(random_state=0), {
'C': np.logspace(-2, 7, 10)
}),
(LinearSVC(random_state=0), {
'C': np.logspace(-2, 7, 10)
}),
(make_pipeline(
KBinsDiscretizer(encode='onehot'),
LogisticRegression(random_state=0)), {
'kbinsdiscretizer__n_bins': np.arange(2, 10),
'logisticregression__C': np.logspace(-2, 7, 10),
}),
(make_pipeline(
KBinsDiscretizer(encode='onehot'), LinearSVC(random_state=0)), {
'kbinsdiscretizer__n_bins': np.arange(2, 10),
'linearsvc__C': np.logspace(-2, 7, 10),
}),
(GradientBoostingClassifier(n_estimators=50, random_state=0), {
'learning_rate': np.logspace(-4, 0, 10)
}),
(SVC(random_state=0), {
'C': np.logspace(-2, 7, 10)
}),
]
names = [get_name(e) for e, g in classifiers]
n_samples = 100
datasets = [
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_classification(n_samples=n_samples, n_features=2, n_redundant=0,
n_informative=2, random_state=2,
n_clusters_per_class=1)
]
fig, axes = plt.subplots(nrows=len(datasets), ncols=len(classifiers) + 1,
figsize=(21, 9))
cm = plt.cm.PiYG
cm_bright = ListedColormap(['#b30065', '#178000'])
# iterate over datasets
for ds_cnt, (X, y) in enumerate(datasets):
print('\ndataset %d\n---------' % ds_cnt)
# preprocess dataset, split into training and test part
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=.5, random_state=42)
# create the grid for background colors
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(
np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# plot the dataset first
ax = axes[ds_cnt, 0]
if ds_cnt == 0:
ax.set_title("Input data")
# plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6,
edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
# iterate over classifiers
for est_idx, (name, (estimator, param_grid)) in \
enumerate(zip(names, classifiers)):
ax = axes[ds_cnt, est_idx + 1]
clf = GridSearchCV(estimator=estimator, param_grid=param_grid)
with ignore_warnings(category=ConvergenceWarning):
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
print('%s: %.2f' % (name, score))
# plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]*[y_min, y_max].
if hasattr(clf, "decision_function"):
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
else:
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
# put the result into a color plot
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
# plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright,
edgecolors='k', alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
if ds_cnt == 0:
ax.set_title(name.replace(' + ', '\n'))
ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0'), size=15,
bbox=dict(boxstyle='round', alpha=0.8, facecolor='white'),
transform=ax.transAxes, horizontalalignment='right')
plt.tight_layout()
# Add suptitles above the figure
plt.subplots_adjust(top=0.90)
suptitles = [
'Linear classifiers',
'Feature discretization and linear classifiers',
'Non-linear classifiers',
]
for i, suptitle in zip([1, 3, 5], suptitles):
ax = axes[0, i]
ax.text(1.05, 1.25, suptitle, transform=ax.transAxes,
horizontalalignment='center', size='x-large')
plt.show()

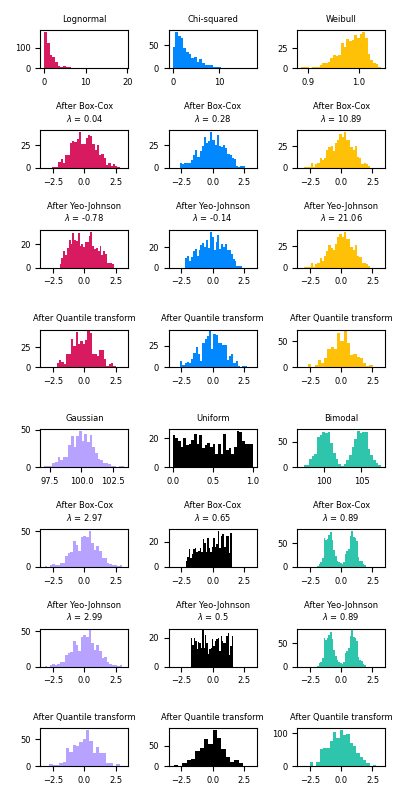
2. Map data to normal distribution
the Box-Cox and Yeo-Johnson transforms through
PowerTransformerto map data from various distributions to a normal distribution. Below are examples of Box-Cox and Yeo-Johnwon applied to six different probability distributions: Lognormal, Chi-squared, Weibull, Gaussian, Uniform, and Bimodal.
- Box-Cox does not support inputs with negative values.
QuantileTransformercan force any arbitrary distribution into a gaussian,
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import QuantileTransformer
from sklearn.model_selection import train_test_split
print(__doc__)
N_SAMPLES = 1000
FONT_SIZE = 6
BINS = 30
rng = np.random.RandomState(304)
bc = PowerTransformer(method='box-cox')
yj = PowerTransformer(method='yeo-johnson')
# n_quantiles is set to the training set size rather than the default value
# to avoid a warning being raised by this example
qt = QuantileTransformer(n_quantiles=500, output_distribution='normal',
random_state=rng)
size = (N_SAMPLES, 1)
# lognormal distribution
X_lognormal = rng.lognormal(size=size)
# chi-squared distribution
df = 3
X_chisq = rng.chisquare(df=df, size=size)
# weibull distribution
a = 50
X_weibull = rng.weibull(a=a, size=size)
# gaussian distribution
loc = 100
X_gaussian = rng.normal(loc=loc, size=size)
# uniform distribution
X_uniform = rng.uniform(low=0, high=1, size=size)
# bimodal distribution
loc_a, loc_b = 100, 105
X_a, X_b = rng.normal(loc=loc_a, size=size), rng.normal(loc=loc_b, size=size)
X_bimodal = np.concatenate([X_a, X_b], axis=0)
# create plots
distributions = [
('Lognormal', X_lognormal),
('Chi-squared', X_chisq),
('Weibull', X_weibull),
('Gaussian', X_gaussian),
('Uniform', X_uniform),
('Bimodal', X_bimodal)
]
colors = ['#D81B60', '#0188FF', '#FFC107',
'#B7A2FF', '#000000', '#2EC5AC']
fig, axes = plt.subplots(nrows=8, ncols=3, figsize=plt.figaspect(2))
axes = axes.flatten()
axes_idxs = [(0, 3, 6, 9), (1, 4, 7, 10), (2, 5, 8, 11), (12, 15, 18, 21),
(13, 16, 19, 22), (14, 17, 20, 23)]
axes_list = [(axes[i], axes[j], axes[k], axes[l])
for (i, j, k, l) in axes_idxs]
for distribution, color, axes in zip(distributions, colors, axes_list):
name, X = distribution
X_train, X_test = train_test_split(X, test_size=.5)
# perform power transforms and quantile transform
X_trans_bc = bc.fit(X_train).transform(X_test)
lmbda_bc = round(bc.lambdas_[0], 2)
X_trans_yj = yj.fit(X_train).transform(X_test)
lmbda_yj = round(yj.lambdas_[0], 2)
X_trans_qt = qt.fit(X_train).transform(X_test)
ax_original, ax_bc, ax_yj, ax_qt = axes
ax_original.hist(X_train, color=color, bins=BINS)
ax_original.set_title(name, fontsize=FONT_SIZE)
ax_original.tick_params(axis='both', which='major', labelsize=FONT_SIZE)
for ax, X_trans, meth_name, lmbda in zip(
(ax_bc, ax_yj, ax_qt),
(X_trans_bc, X_trans_yj, X_trans_qt),
('Box-Cox', 'Yeo-Johnson', 'Quantile transform'),
(lmbda_bc, lmbda_yj, None)):
ax.hist(X_trans, color=color, bins=BINS)
title = 'After {}'.format(meth_name)
if lmbda is not None:
title += '\n$\\lambda$ = {}'.format(lmbda)
ax.set_title(title, fontsize=FONT_SIZE)
ax.tick_params(axis='both', which='major', labelsize=FONT_SIZE)
ax.set_xlim([-3.5, 3.5])
plt.tight_layout()
plt.show()
3. KBinsDiscretizer
make linear model more powerful on continuous data is to use discretization (also known as binning). In the example, we discretize the feature and one-hot encode the transformed data. Note that if the bins are not reasonably wide, there would appear to be a substantially increased risk of overfitting, so the discretizer parameters should usually be tuned under cross validation.
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = LinearRegression().fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color='green',
label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color='red',
label="decision tree")
ax1.plot(X[:, 0], y, 'o', c='k')
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")
# predict with transformed dataset
line_binned = enc.transform(line)
reg = LinearRegression().fit(X_binned, y)
ax2.plot(line, reg.predict(line_binned), linewidth=2, color='green',
linestyle='-', label='linear regression')
reg = DecisionTreeRegressor(min_samples_split=3,
random_state=0).fit(X_binned, y)
ax2.plot(line, reg.predict(line_binned), linewidth=2, color='red',
linestyle=':', label='decision tree')
ax2.plot(X[:, 0], y, 'o', c='k')
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=.2)
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")
plt.tight_layout()
plt.show()

.1. Strateges
- ‘uniform’: The discretization is uniform in each feature, which means that the bin widths are constant in each dimension.
- quantile’: The discretization is done on the quantiled values, which means that each bin has approximately the same number of samples.
- ‘kmeans’: The discretization is based on the centroids of a KMeans clustering procedure.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.datasets import make_blobs
print(__doc__)
strategies = ['uniform', 'quantile', 'kmeans']
n_samples = 200
centers_0 = np.array([[0, 0], [0, 5], [2, 4], [8, 8]])
centers_1 = np.array([[0, 0], [3, 1]])
# construct the datasets
random_state = 42
X_list = [
np.random.RandomState(random_state).uniform(-3, 3, size=(n_samples, 2)),
make_blobs(n_samples=[n_samples // 10, n_samples * 4 // 10,
n_samples // 10, n_samples * 4 // 10],
cluster_std=0.5, centers=centers_0,
random_state=random_state)[0],
make_blobs(n_samples=[n_samples // 5, n_samples * 4 // 5],
cluster_std=0.5, centers=centers_1,
random_state=random_state)[0],
]
figure = plt.figure(figsize=(14, 9))
i = 1
for ds_cnt, X in enumerate(X_list):
ax = plt.subplot(len(X_list), len(strategies) + 1, i)
ax.scatter(X[:, 0], X[:, 1], edgecolors='k')
if ds_cnt == 0:
ax.set_title("Input data", size=14)
xx, yy = np.meshgrid(
np.linspace(X[:, 0].min(), X[:, 0].max(), 300),
np.linspace(X[:, 1].min(), X[:, 1].max(), 300))
grid = np.c_[xx.ravel(), yy.ravel()]
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
i += 1
# transform the dataset with KBinsDiscretizer
for strategy in strategies:
enc = KBinsDiscretizer(n_bins=4, encode='ordinal', strategy=strategy)
enc.fit(X)
grid_encoded = enc.transform(grid)
ax = plt.subplot(len(X_list), len(strategies) + 1, i)
# horizontal stripes
horizontal = grid_encoded[:, 0].reshape(xx.shape)
ax.contourf(xx, yy, horizontal, alpha=.5)
# vertical stripes
vertical = grid_encoded[:, 1].reshape(xx.shape)
ax.contourf(xx, yy, vertical, alpha=.5)
ax.scatter(X[:, 0], X[:, 1], edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
if ds_cnt == 0:
ax.set_title("strategy='%s'" % (strategy, ), size=14)
i += 1
plt.tight_layout()
plt.show()

4. Feature Scaling
.1. StandardScaler
Standardization involves rescaling the features such that they have the properties of a standard normal distribution with a mean of zero and a standard deviation of one.
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.naive_bayes import GaussianNB
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.pipeline import make_pipeline
print(__doc__)
# Code source: Tyler Lanigan <tylerlanigan@gmail.com>
# Sebastian Raschka <mail@sebastianraschka.com>
# License: BSD 3 clause
RANDOM_STATE = 42
FIG_SIZE = (10, 7)
features, target = load_wine(return_X_y=True)
# Make a train/test split using 30% test size
X_train, X_test, y_train, y_test = train_test_split(features, target,
test_size=0.30,
random_state=RANDOM_STATE)
# Fit to data and predict using pipelined GNB and PCA.
unscaled_clf = make_pipeline(PCA(n_components=2), GaussianNB())
unscaled_clf.fit(X_train, y_train)
pred_test = unscaled_clf.predict(X_test)
# Fit to data and predict using pipelined scaling, GNB and PCA.
std_clf = make_pipeline(StandardScaler(), PCA(n_components=2), GaussianNB())
std_clf.fit(X_train, y_train)
pred_test_std = std_clf.predict(X_test)
# Show prediction accuracies in scaled and unscaled data.
print('\nPrediction accuracy for the normal test dataset with PCA')
print('{:.2%}\n'.format(metrics.accuracy_score(y_test, pred_test)))
print('\nPrediction accuracy for the standardized test dataset with PCA')
print('{:.2%}\n'.format(metrics.accuracy_score(y_test, pred_test_std)))
# Extract PCA from pipeline
pca = unscaled_clf.named_steps['pca']
pca_std = std_clf.named_steps['pca']
# Show first principal components
print('\nPC 1 without scaling:\n', pca.components_[0])
print('\nPC 1 with scaling:\n', pca_std.components_[0])
# Use PCA without and with scale on X_train data for visualization.
X_train_transformed = pca.transform(X_train)
scaler = std_clf.named_steps['standardscaler']
X_train_std_transformed = pca_std.transform(scaler.transform(X_train))
# visualize standardized vs. untouched dataset with PCA performed
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=FIG_SIZE)
for l, c, m in zip(range(0, 3), ('blue', 'red', 'green'), ('^', 's', 'o')):
ax1.scatter(X_train_transformed[y_train == l, 0],
X_train_transformed[y_train == l, 1],
color=c,
label='class %s' % l,
alpha=0.5,
marker=m
)
for l, c, m in zip(range(0, 3), ('blue', 'red', 'green'), ('^', 's', 'o')):
ax2.scatter(X_train_std_transformed[y_train == l, 0],
X_train_std_transformed[y_train == l, 1],
color=c,
label='class %s' % l,
alpha=0.5,
marker=m
)
ax1.set_title('Training dataset after PCA')
ax2.set_title('Standardized training dataset after PCA')
for ax in (ax1, ax2):
ax.set_xlabel('1st principal component')
ax.set_ylabel('2nd principal component')
ax.legend(loc='upper right')
ax.grid()
plt.tight_layout()
plt.show()

.2. Different Scalers
import numpy as np
import matplotlib as mpl
from matplotlib import pyplot as plt
from matplotlib import cm
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import minmax_scale
from sklearn.preprocessing import MaxAbsScaler
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import PowerTransformer
from sklearn.datasets import fetch_california_housing
print(__doc__)
dataset = fetch_california_housing()
X_full, y_full = dataset.data, dataset.target
# Take only 2 features to make visualization easier
# Feature of 0 has a long tail distribution.
# Feature 5 has a few but very large outliers.
X = X_full[:, [0, 5]]
distributions = [
('Unscaled data', X),
('Data after standard scaling',
StandardScaler().fit_transform(X)),
('Data after min-max scaling',
MinMaxScaler().fit_transform(X)),
('Data after max-abs scaling',
MaxAbsScaler().fit_transform(X)),
('Data after robust scaling',
RobustScaler(quantile_range=(25, 75)).fit_transform(X)),
('Data after power transformation (Yeo-Johnson)',
PowerTransformer(method='yeo-johnson').fit_transform(X)),
('Data after power transformation (Box-Cox)',
PowerTransformer(method='box-cox').fit_transform(X)),
('Data after quantile transformation (uniform pdf)',
QuantileTransformer(output_distribution='uniform')
.fit_transform(X)),
('Data after quantile transformation (gaussian pdf)',
QuantileTransformer(output_distribution='normal')
.fit_transform(X)),
('Data after sample-wise L2 normalizing',
Normalizer().fit_transform(X)),
]
# scale the output between 0 and 1 for the colorbar
y = minmax_scale(y_full)
# plasma does not exist in matplotlib < 1.5
cmap = getattr(cm, 'plasma_r', cm.hot_r)
def create_axes(title, figsize=(16, 6)):
fig = plt.figure(figsize=figsize)
fig.suptitle(title)
# define the axis for the first plot
left, width = 0.1, 0.22
bottom, height = 0.1, 0.7
bottom_h = height + 0.15
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter = plt.axes(rect_scatter)
ax_histx = plt.axes(rect_histx)
ax_histy = plt.axes(rect_histy)
# define the axis for the zoomed-in plot
left = width + left + 0.2
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter_zoom = plt.axes(rect_scatter)
ax_histx_zoom = plt.axes(rect_histx)
ax_histy_zoom = plt.axes(rect_histy)
# define the axis for the colorbar
left, width = width + left + 0.13, 0.01
rect_colorbar = [left, bottom, width, height]
ax_colorbar = plt.axes(rect_colorbar)
return ((ax_scatter, ax_histy, ax_histx),
(ax_scatter_zoom, ax_histy_zoom, ax_histx_zoom),
ax_colorbar)
def plot_distribution(axes, X, y, hist_nbins=50, title="",
x0_label="", x1_label=""):
ax, hist_X1, hist_X0 = axes
ax.set_title(title)
ax.set_xlabel(x0_label)
ax.set_ylabel(x1_label)
# The scatter plot
colors = cmap(y)
ax.scatter(X[:, 0], X[:, 1], alpha=0.5, marker='o', s=5, lw=0, c=colors)
# Removing the top and the right spine for aesthetics
# make nice axis layout
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.spines['left'].set_position(('outward', 10))
ax.spines['bottom'].set_position(('outward', 10))
# Histogram for axis X1 (feature 5)
hist_X1.set_ylim(ax.get_ylim())
hist_X1.hist(X[:, 1], bins=hist_nbins, orientation='horizontal',
color='grey', ec='grey')
hist_X1.axis('off')
# Histogram for axis X0 (feature 0)
hist_X0.set_xlim(ax.get_xlim())
hist_X0.hist(X[:, 0], bins=hist_nbins, orientation='vertical',
color='grey', ec='grey')
hist_X0.axis('off')
# 不同的scale 处理效果
def make_plot(item_idx):
title, X = distributions[item_idx]
ax_zoom_out, ax_zoom_in, ax_colorbar = create_axes(title)
axarr = (ax_zoom_out, ax_zoom_in)
plot_distribution(axarr[0], X, y, hist_nbins=200,
x0_label="Median Income",
x1_label="Number of households",
title="Full data")
# zoom-in
zoom_in_percentile_range = (0, 99)
cutoffs_X0 = np.percentile(X[:, 0], zoom_in_percentile_range)
cutoffs_X1 = np.percentile(X[:, 1], zoom_in_percentile_range)
non_outliers_mask = (
np.all(X > [cutoffs_X0[0], cutoffs_X1[0]], axis=1) &
np.all(X < [cutoffs_X0[1], cutoffs_X1[1]], axis=1))
plot_distribution(axarr[1], X[non_outliers_mask], y[non_outliers_mask],
hist_nbins=50,
x0_label="Median Income",
x1_label="Number of households",
title="Zoom-in")
norm = mpl.colors.Normalize(y_full.min(), y_full.max())
mpl.colorbar.ColorbarBase(ax_colorbar, cmap=cmap,
norm=norm, orientation='vertical',
label='Color mapping for values of y')
.1. MinMaxScaler
MinMaxScalerrescales the data set such that all feature values are in the range [0, 1] as shown in the right panel below.
.2. StandScaler
StandardScalerremoves the mean and scales the data to unit variance.
.3. MaxAbsScaler
MaxAbsScaleris similar toMinMaxScalerexcept that the values are mapped in the range [0, 1]. On positive only data, both scalers behave similarly.MaxAbsScalertherefore also suffers from the presence of large outliers.
.4. RobustScaler
the centering and scaling statistics of
RobustScalerisbased on percentilesand are thereforenot influenced by a few number of very large marginal outliers.
.5. PowerTransformer
PowerTransformerapplies a power transformation to each feature to make the datamore Gaussian-like in ordertostabilize variance and minimize skewness.
.6. QuantileTransformer
QuantileTransformerapplies anon-linear transformationsuch that the probability density function of each feature will be mapped to auniform or Gaussian distribution. In this case, all the data, including outliers, will be mapped to a uniform distribution with the range [0, 1], making outliers indistinguishable from inliers.
.7. Normalizer
The
Normalizerrescales the vector for each sample to have unit norm, independently of the distribution of the samples.